El Análisis de Vecindad de Kriging (Kriging Neighborhood Analysis, KNA) en geología es un método geoestadístico utilizado para optimizar los parámetros del kriging, una técnica de estimación geoestadística, con el fin de mejorar la precisión y confiabilidad de las estimaciones de recursos minerales. Específicamente, el KNA ayuda a minimizar el sesgo condicional, un problema común en el kriging donde las leyes estimadas de los bloques presentan menor variabilidad que las leyes reales.

La mayoría de los métodos de estimación de recursos utilizan alguna forma de suavizado de leyes para interpolar valores en un bloque basándose en las muestras circundantes. El proceso de determinar un esquema de búsqueda de muestras adecuado se denomina frecuentemente análisis de vecindad de kriging, y una guía para su implementación se presenta en Vann, Jackson y Bertoli (2003). Estos métodos pueden dividirse en dos categorías: no geoestadísticos y geoestadísticos.

Los métodos no geoestadísticos de interpolación de leyes utilizan alguna relación entre la distancia de una muestra al centro del bloque y el peso asignado a ella. El enfoque más utilizado pondera cada muestra por alguna potencia del inverso de su distancia al bloque que se está estimando (IDW, por sus siglas en inglés).

Todos los enfoques geoestadísticos para la interpolación de leyes se basan en alguna forma de kriging, donde el peso aplicado a cada muestra se basa en un modelo de semivariograma que define la continuidad espacial. Estos métodos geoestadísticos pueden dividirse en tres clases: kriging lineal, kriging no lineal y modelado por simulación.

Los métodos de kriging lineal son los más fáciles de aplicar y se basan en el kriging simple u ordinario y sus variaciones. Al modelar recursos mediante kriging, se deben establecer varios parámetros de estimación, como el tamaño de bloque del modelo de bloques, el número mínimo y máximo de muestras, etc.

Si la interpolación de leyes en un bloque del modelo de bloques se realizó utilizando el método de kriging ordinario o simple, entonces para categorizar los recursos es necesario calcular varios atributos que muestran la calidad de los resultados de la estimación para cada bloque (incluyendo la presencia de una estimación sesgada).

En la mayoría de los productos de software modernos, estos parámetros se calculan automáticamente. Diferentes paquetes de software incorporan la funcionalidad KNA para asistir a los geólogos en este proceso. Con el lanzamiento de K-MINE 2025, el Análisis de Vecindad de Kriging (KNA) está ahora disponible al realizar análisis geoestadísticos.

En este artículo, examinaremos las principales métricas del KNA y su impacto en la estimación de recursos.

Principales métricas del KNA

Para evaluar el desempeño del kriging, se emplea un conjunto de métricas denominadas colectivamente Análisis de Vecindad de Kriging (KNA), tales como la varianza de kriging, la eficiencia de kriging, la pendiente de regresión, la magnitud de los pesos negativos, etc. Al optimizar estos parámetros, el KNA busca minimizar el sesgo condicional, que es la diferencia entre las leyes estimadas de los bloques y la ley promedio real de los bloques explotados.

Optimización del tamaño de bloque

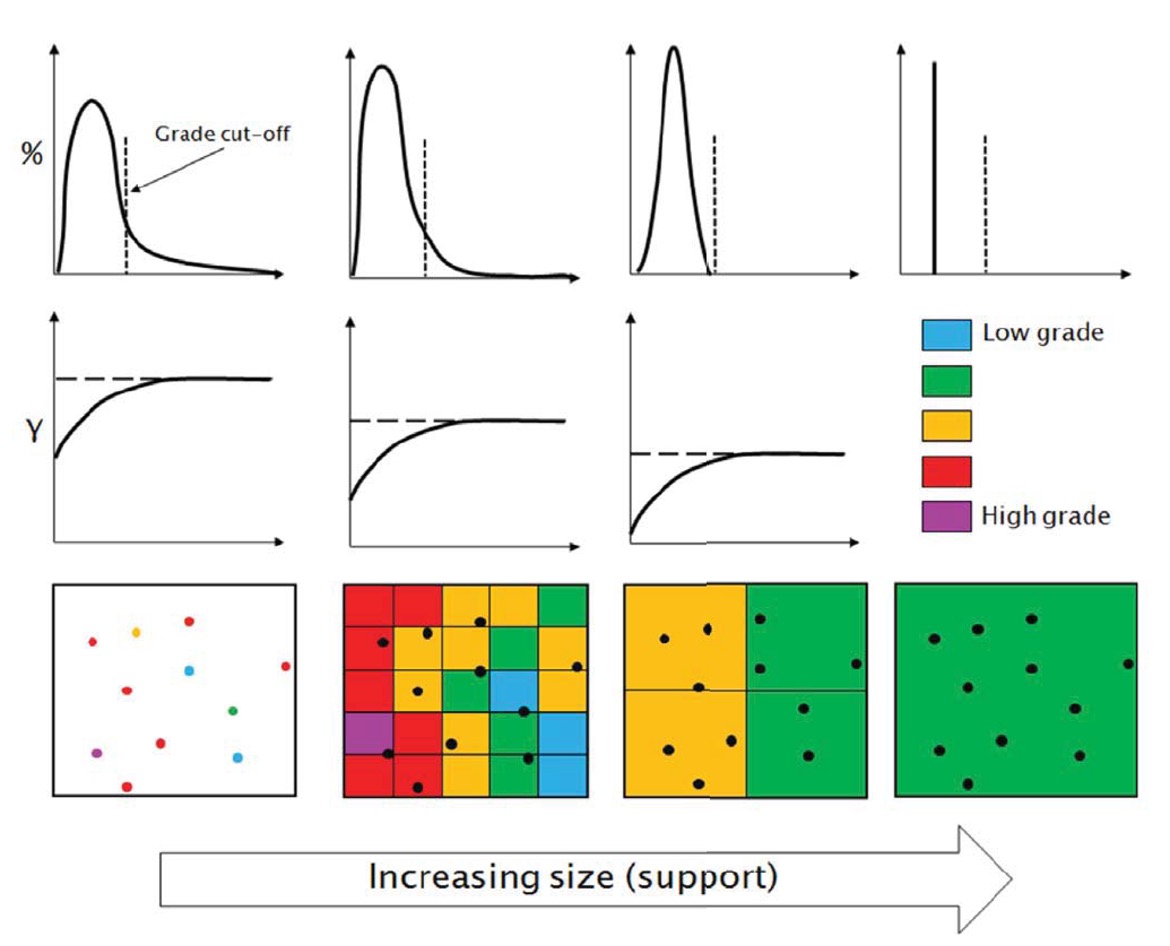
FIG. 1 – Ilustración del efecto volumen-varianza o el cambio de soporte desde puntos hasta el dominio completo sobre la distribución de leyes y el variograma

La determinación del tamaño de bloque requiere una evaluación cuidadosa de muchos factores, incluyendo consideraciones de ingeniería, geometría del depósito mineral, tamaño de los equipos y espaciamiento de los datos. La Figura 2 muestra que, basándose en la eficiencia de kriging y la pendiente de regresión, el tamaño de bloque óptimo es 80×80×40.

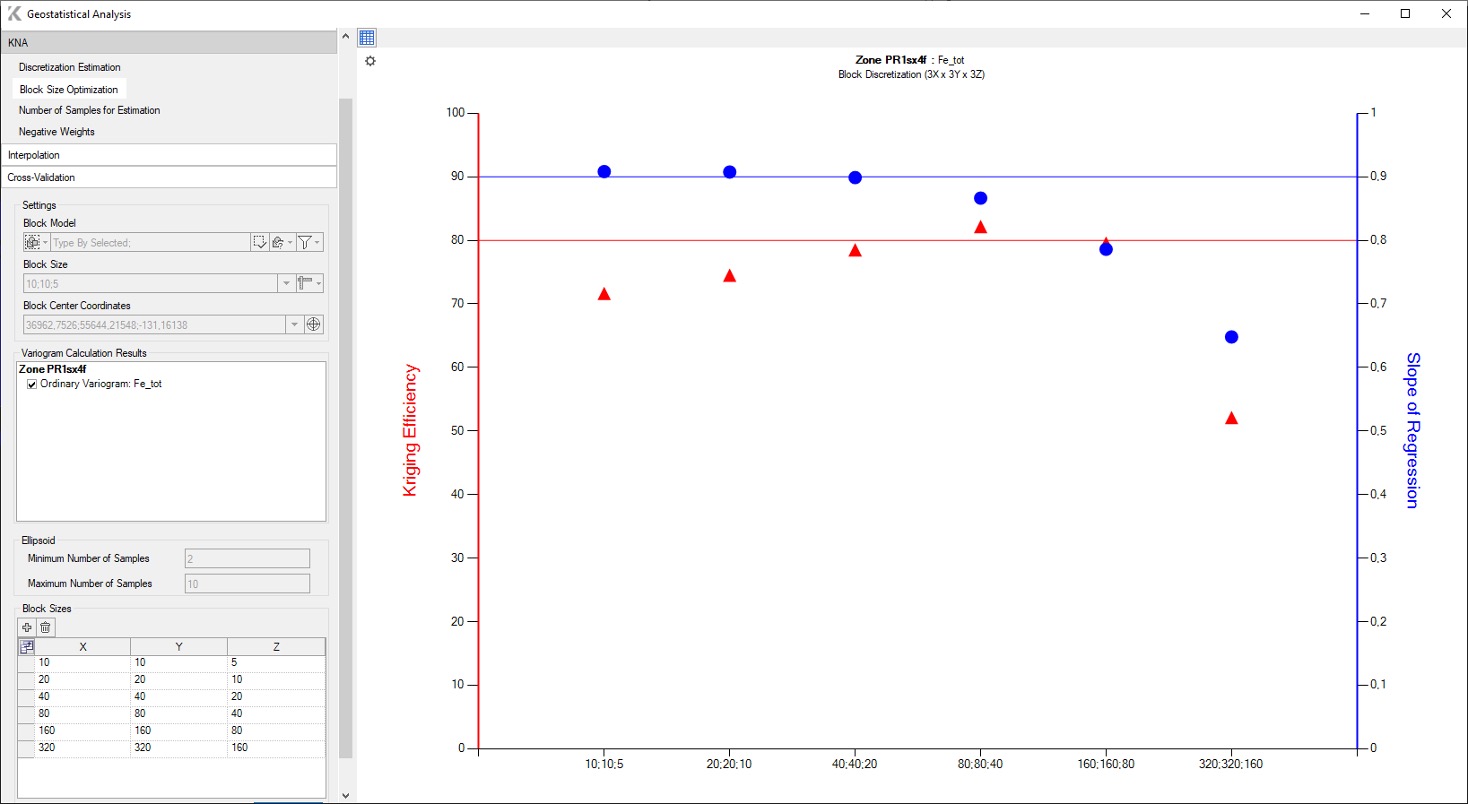
FIG. 2 – Optimización del tamaño de bloque en K-MINE

Sin embargo, debe recordarse que el concepto de «óptimo» debe definirse para cada situación. La discusión debe pasar del sesgo condicional al propósito de la estimación y los objetivos del estudio.

Eficiencia de kriging

La Eficiencia de Kriging (KE, por sus siglas en inglés) fue introducida por Krige (1996) como una métrica para evaluar la eficiencia de las estimaciones de bloques. La ecuación para KE es:

donde KV es la varianza de kriging y BV es la varianza del bloque.

La ecuación para BV es:

donde μ es el multiplicador de Lagrange, λi son los coeficientes de kriging, γ(xi,xo) es el valor del variograma para las distancias en pares: muestra-ubicación de estimación (centro del bloque).

Una KE alta indica una KV baja, lo que señala la presencia de numerosos puntos de datos espaciados cercanamente y un suavizado mínimo en la estimación. Por el contrario, una KE baja implica una KV alta, lo que sugiere escasez de datos locales y el potencial de una estimación suavizada.

Varianza de kriging

La varianza de kriging es el error minimizado de la estimación de kriging, es decir, la diferencia cuadrática esperada entre el valor real y el valor estimado. La varianza de kriging se calcula utilizando los valores de covarianza (obtenidos del variograma) y los pesos asignados a los puntos de datos en el espacio de búsqueda (Barboza I. y Deutsch C., 2024). La ecuación para KV es:

donde μ es el multiplicador de Lagrange, λi son los coeficientes de kriging, γ(xi,V) es el valor medio aritmético de γ a lo largo del variograma para las distancias a todos los puntos de muestreo en el bloque desde el punto xi, γ(V,V) es el valor medio aritmético de γ a lo largo del variograma entre todos los puntos de muestreo dentro del bloque.

La KV, en conjunto con la Eficiencia de Kriging, constituye un conjunto de parámetros estrechamente interrelacionados para evaluar el desempeño del kriging.

El cálculo de la KV está estrechamente relacionado con la discretización, ya que requiere el cálculo del gamma promedio sobre los puntos de discretización en un bloque, y no solo sobre el punto central del bloque, como en el cálculo de BV.

El principio de discretización consiste en estimar el valor promedio dentro de un área local especificada (en K-MINE, dentro de un bloque virtual, cuyas coordenadas del centro y dimensiones se especifican en la configuración inicial).

Para esto, el usuario debe especificar el número de puntos discretos dentro del bloque. Los puntos de discretización son los centros de las celdas dentro del bloque estimado (FIG. 3). Cada punto se estima (como una estimación puntual), y el valor promedio de estos puntos es la estimación del bloque. El número de puntos de discretización corresponde al número de celdas en las que se divide el bloque.

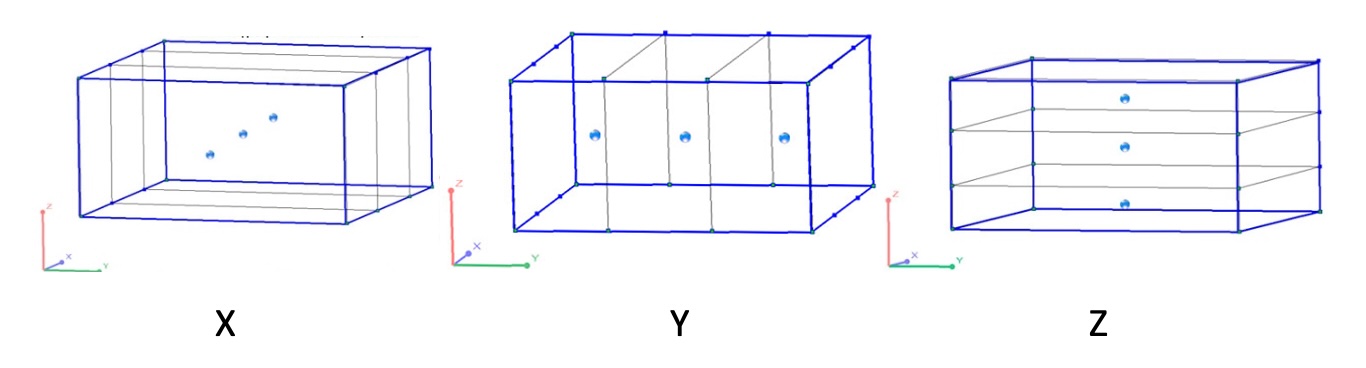
FIG. 3 – Número de puntos de discretización en las direcciones de los ejes en K-MINE

El tamaño inicial del bloque y las coordenadas de su centro son especificados por el usuario. Luego, dependiendo del número de puntos discretos especificados, el bloque original se divide equitativamente en el número correspondiente de celdas en las direcciones X, Y y Z, y las coordenadas de los centros de los subbloques formados corresponderán a los puntos de discretización. Es decir, el número de puntos discretos determina el número de subbloques.

Por ejemplo, si para un bloque inicial con tamaño de arista a lo largo de los ejes X, Y y Z de 10×10×5, se especifica la combinación de puntos discretos: en la dirección X=3, en la dirección Y=3, en la dirección Z=3. Esto significa que el bloque se divide uniformemente en tres celdas a lo largo de tres ejes. El tamaño de arista de los subbloques es: para X=10/3=3,33 m, para Y=10/3=3,33 m, para Z=5/3=1,66 m, y el número de puntos discretos (centros de subbloques) en el bloque inicial será: 3×3×3=27.

El gráfico en la Fig. 4 muestra una línea horizontal en rojo, correspondiente a un valor de Eficiencia de Kriging del 80%. Esta línea sirve como guía para el usuario al elegir el número óptimo de puntos de muestreo.

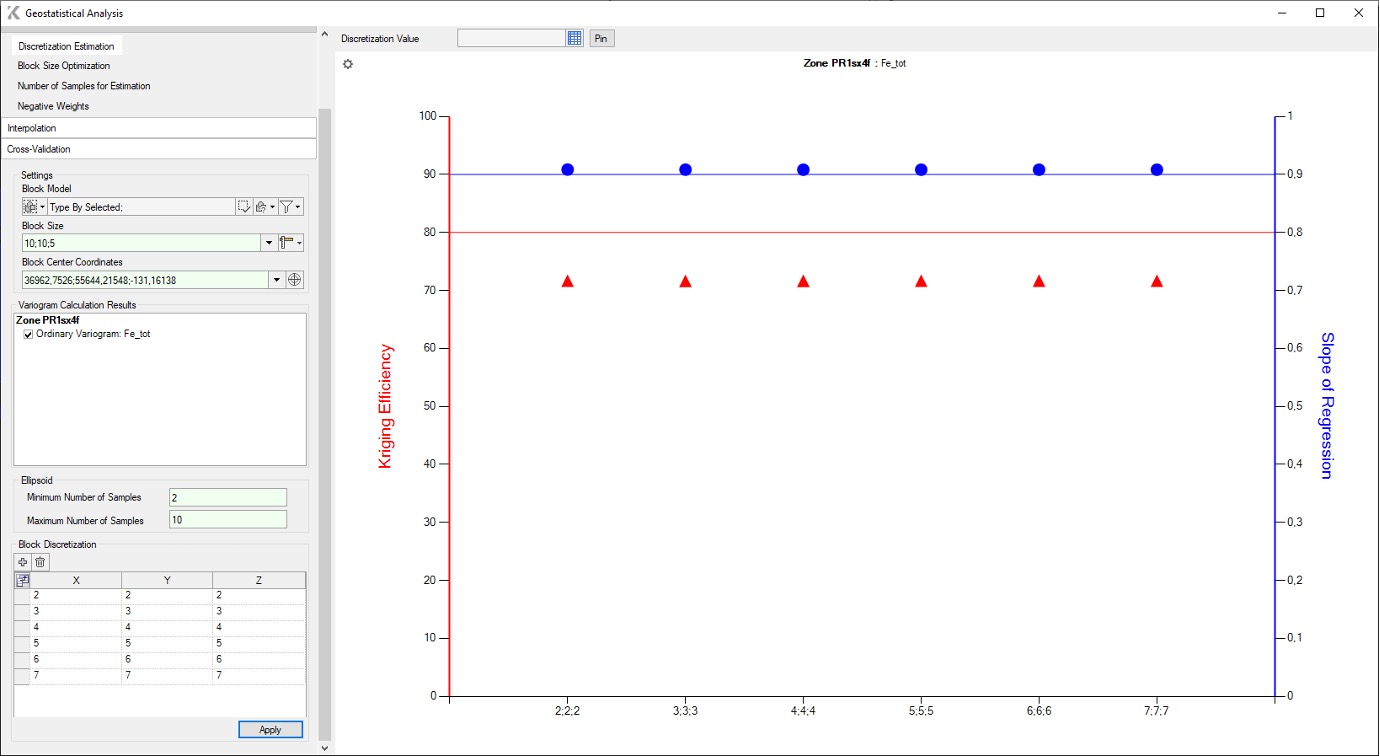
FIG. 4 – Estimación de discretización en K-MINE

La opción de discretización óptima se determina por los puntos en el gráfico ubicados lo más cerca posible de las líneas roja (eficiencia de kriging 80%) y azul (pendiente de regresión 0,9).

Pendiente de regresión

La Pendiente de Regresión (SR, por sus siglas en inglés) proporciona una medida del sesgo condicional, midiendo la pendiente de la regresión lineal del valor real sobre la estimación. Esto se observa directamente en la validación cruzada, pero también puede calcularse teóricamente bloque por bloque utilizando valores esperados derivados de las covarianzas.

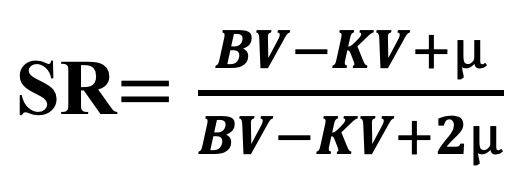
donde µ es el multiplicador de Lagrange al calcular KV.

La pendiente de la línea de regresión, que relaciona los valores reales y estimados, se utiliza frecuentemente para diagnosticar el sesgo condicional. Idealmente, la pendiente de esta línea debería ser igual a uno, lo que implica ausencia de sesgo condicional.

Tanto la pendiente de regresión como la eficiencia de kriging deben tratarse con precaución. La reducción del sesgo calculado puede no ser un enfoque apropiado para estimar leyes de metal, especialmente en depósitos que requieren leyes de corte altas para su extracción.

El sesgo condicional es un problema serio si la estimación se va a utilizar para tomar una decisión final o casi final, como para el control de leyes en una mina a cielo abierto o para estimar caserones en minería subterránea. Si la estimación está destinada a separar estéril y mineral al final de la producción, entonces el suavizado está justificado para prevenir el sesgo condicional.

Sin embargo, si sus estimaciones de ley están destinadas a una etapa de planificación intermedia y en el futuro habrá información más detallada disponible para separar mineral y estéril en condiciones de producción, entonces el suavizado será un problema porque no reflejará la relación correcta ley-tonelaje que se puede esperar durante la producción (Glacken I. y Trueman A., 2014).

Número de muestras para estimación y pesos negativos

El cálculo de estos indicadores se realiza para confirmar la elección óptima de la estimación de kriging insesgada con el tamaño de bloque óptimo.

Al hacer clic en un marcador, los valores correspondientes se visualizan en el gráfico, y el usuario debe seleccionar y fijar los valores máximo y mínimo de muestras más aceptables (FIG. 5).

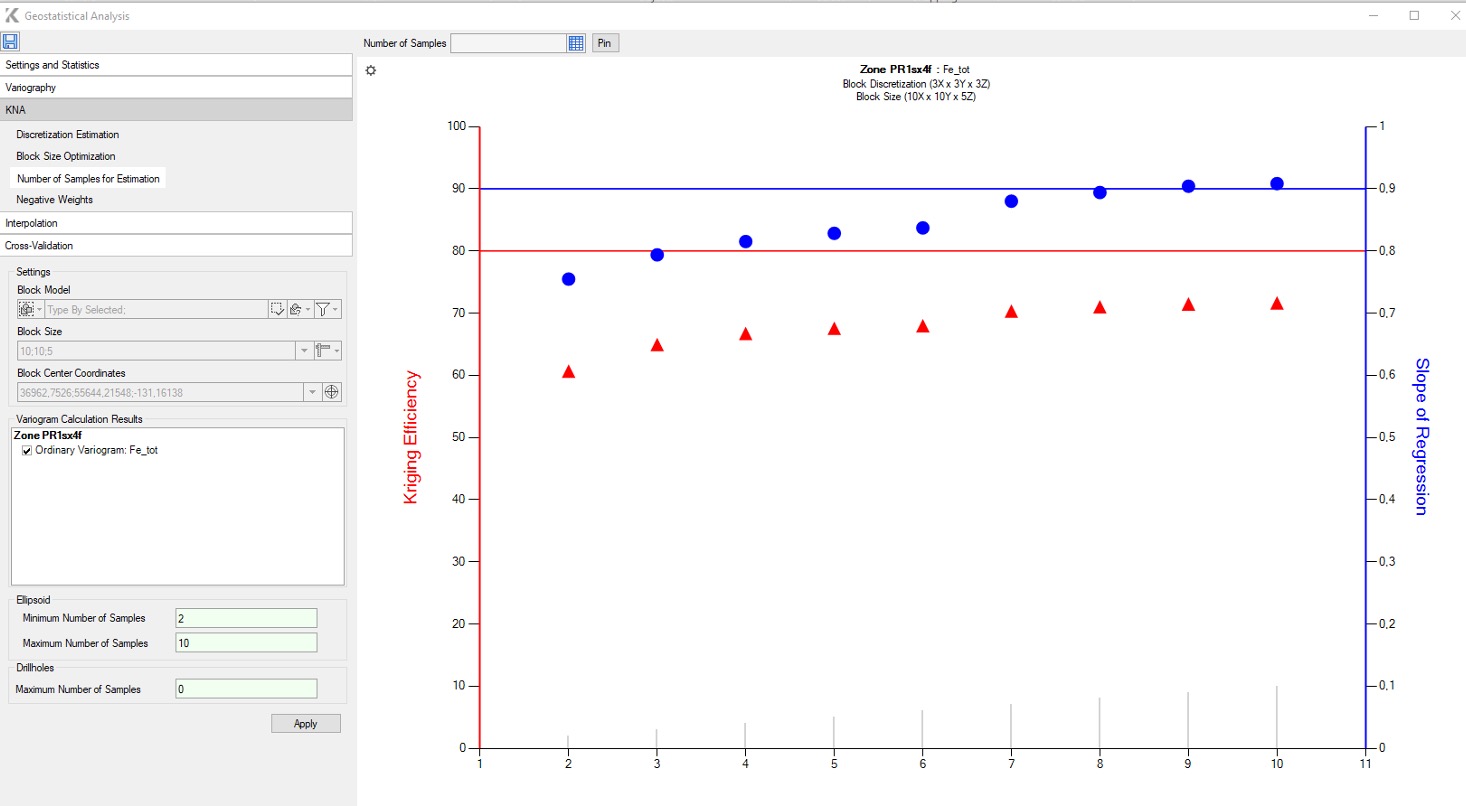
FIG. 5 – Estimación del número de muestras en K-MINE

En el marco de la interpolación, pueden aparecer pesos de kriging negativos en el límite de búsqueda. Su presencia indica la selección de parámetros de interpolación confiables, pero su cantidad en la masa total de muestras que participan en la interpolación no debe exceder el 5%. Si la cantidad de pesos excede el valor especificado, existe el riesgo de obtener un resultado poco confiable.

En zonas de menor densidad de muestreo o donde no hay muestreo, está presente al menos un peso negativo. El espacio en blanco en el mapa representa bloques donde solo hay pesos positivos. En el Kriging Simple, la Pendiente de Regresión siempre es igual a uno.

El cálculo del número de pesos de kriging negativos y la suma de pesos negativos en K-MINE se realiza para todos los tamaños de bloque especificados en la pestaña «Optimización del tamaño de bloque» con las configuraciones previamente seleccionadas y fijadas: el número de puntos de muestreo, el número mínimo y máximo de muestras, y el número mínimo de muestras de un sondaje (FIG. 6).

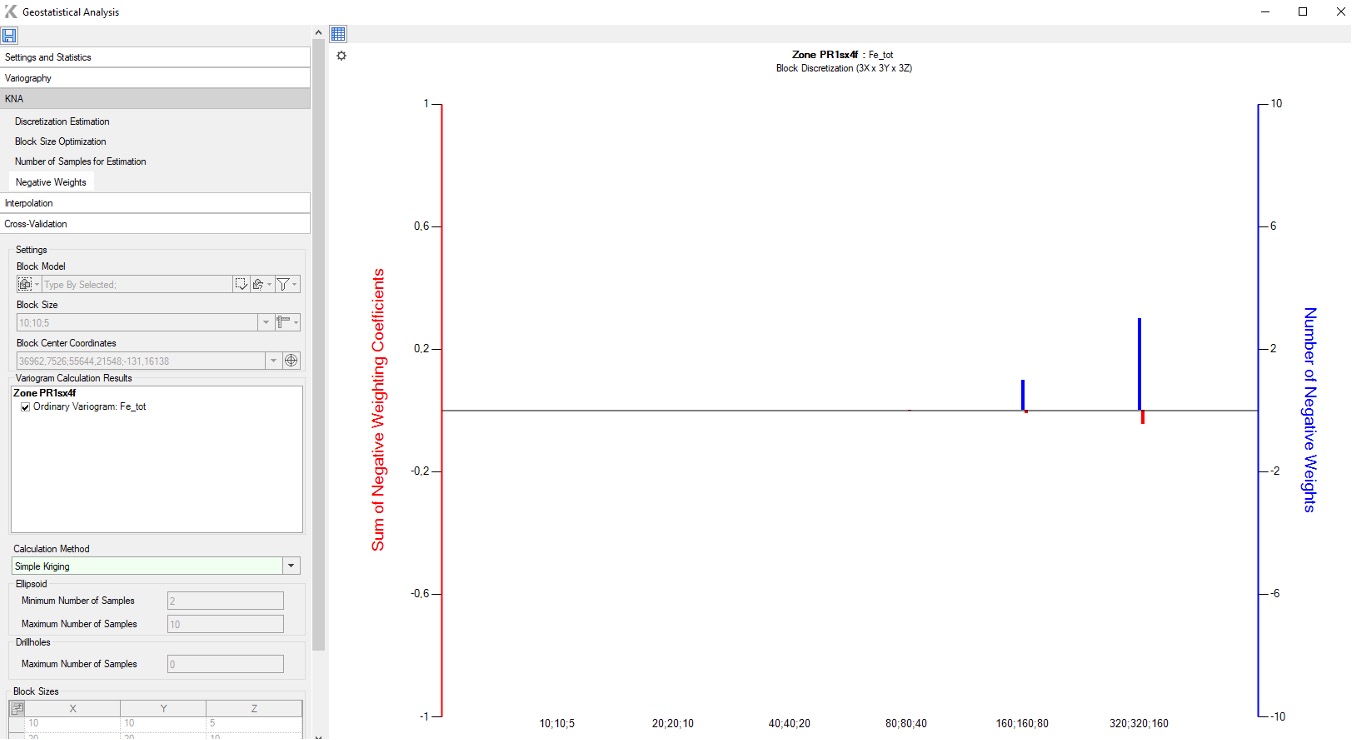
FIG. 6 – Estimación de pesos negativos en K-MINE

Después de aceptar los parámetros apropiados, los usuarios pueden proceder a las siguientes etapas de interpolación y validación del modelo de bloques. K-MINE soporta Kriging Simple y Ordinario, Kriging con deriva externa, Cokriging, etc.

Discusión

El KNA puede integrarse en los flujos de trabajo de estimación de recursos, permitiendo a los geólogos optimizar parámetros directamente dentro del software y aplicar estas configuraciones optimizadas a la estimación final de leyes. Los geólogos enfrentan constantemente el desafío de proporcionar estimaciones de recursos precisas de manera más rápida, mejor o más económica.

Por un lado, el software ayuda a implementar múltiples iteraciones más rápidamente, pero al mismo tiempo, crece la necesidad de comprender los métodos geoestadísticos y la interacción con muchas otras disciplinas. La relación entre la ley de corte, el variograma, el espaciamiento de muestreo, el grado de suavizado requerido y la selectividad de recuperación estimada es un problema complejo.

Incluyendo factores de geometalurgia, geotecnia, etc. en la estimación del modelo, un geólogo debe tener conocimientos en estas áreas. La tecnología computacional potente es una buena herramienta solo en manos de un profesional.

Existe un debate dentro de la comunidad de estimación de recursos sobre dos objetivos opuestos: minimizar el sesgo condicional global y asegurar la precisión local del bloque. En entornos de alta densidad de muestreo, ambos objetivos son alcanzables, pero en las etapas de pre-desarrollo y factibilidad de un ciclo minero, rara vez es posible minimizar simultáneamente el sesgo global y asegurar la precisión local de la ley. Krige (1996) discute herramientas para medir (y así minimizar) el sesgo condicional en una estimación, mientras que Isaaks (2004) discute la paradoja de intentar lograr una estimación insesgada pero localmente precisa. En opinión de Glacken y Trueman (2014), la mayoría de los estimadores logran alcanzar una estimación condicionalmente insesgada o localmente precisa, y para la mayoría, el enfoque está en lograr un sesgo condicional mínimo a expensas de la precisión local.

La tarea final de la estimación de recursos es asignar categorías de clasificación para la confianza de los recursos. Es bastante común escuchar debates entre geólogos sobre los parámetros del modelo de bloques que deben tenerse en cuenta al asignar categorías de recursos a Medidos, Indicados e Inferidos.

En los métodos poligonales, los recursos generalmente se clasifican utilizando la densidad total de perforación. Otro enfoque es tomar en cuenta la distancia promedio desde el centro del bloque de las muestras utilizadas para estimar el bloque, o simplemente el número de muestras identificadas en el volumen de búsqueda. Esto implica múltiples corridas de estimación y el aumento del radio de búsqueda de las muestras. En este caso, los bloques se estiman utilizando las muestras más distantes con la categoría de confianza más baja. La desventaja de este enfoque automatizado es el infame efecto de «perro manchado» y la violación del requisito necesario de continuidad del cuerpo mineralizado.

También son populares los enfoques para clasificar categorías de recursos basados en la varianza de kriging o el error introducido durante la estimación. La varianza de kriging es un buen indicador de la distancia total entre muestras, considerando la anisotropía y el agrupamiento de muestras. Otros enfoques numéricos incluyen el coeficiente de regresión y los índices de eficiencia de kriging propuestos por Krige.

Para resumir todo lo anterior, la clasificación de recursos se basa en una combinación de criterios numéricos y geológicos con la supervisión necesaria de una persona competente.

El desarrollo del modelado condicional y el uso de tecnología computacional potente e inteligencia artificial abren nuevas perspectivas para la creación de módulos complejos universales que combinan el modelado de recursos con la optimización y planificación de operaciones mineras. Esta es la dirección en la que avanza K-MINE.